当サイトは、アフィリエイト広告を利用しています
【Python × 機械学習】素人が機械学習の基本を単回帰分析でまとめる
Pythonを使った機械学習の基本的な仕組みや
用語をPythonの機械学習ライブラリである「cikit-learn」を
使った簡単な実装を例にして素人がまとめてみる
機械学習には大きく分けて
- 教師あり学習
- 教師なし学習
- 強化学習
がある。
今回は機械学習の基本として教師あり学習の
- 単回帰分析
を例にして説明してみる
機械学習の基本的な知識を得るには下記の書籍が
おすすめです

機械学習の用語
まず機械学習において、最初に「よくわからん!」となるのがややこしい用語がたくさんあり、
しかもそれぞれが別名を持ってたりするので、
書籍やサイトをみていてもどれのことかわからなくなるというのがあるのでまとめておく。
機械学習モデル
一般的にはモデルと表記されることが多い
数理モデルとかAIモデルの時もある
数式でパターンやルールを表現したものがモデルと呼ばれる
モデルは作成時にどの機械学習アルゴリズムで作るかをデータによって判断する
またモデルは学習させるまでは不完全であり数式のパラメータが定まってない状態。
機械学習モデルは
- 機械学習アルゴリズム
- 説明変数
- 目的関数
- パラメータ(パラメータは学習後に定まる)
を元に作成される
機械学習アルゴリズム
機械学習アルゴリズムは、
モデルが学習と予測をどのように行うかを表す手順のこと。
- 回帰分析
- 重回帰分析
- ランダムフォレスト
などがある
パラメータ
モデルの学習実行後に獲得する値。
モデルに学習させるのはこのパラメータを得るため
学習済みモデル
モデルにデータを入れて学習させれば機械学習モデルが完成する。
学習によりパラメータが定まり、数式が完成した状態のこと
完成したモデルに新規のデータを入れれば完成した数式で
計算して予測値を出してくれる。
これを学習済みモデルという
説明変数
モデルに入れるデータのこと
モデルで予測値を出すために使用するデータのこと
目的変数
モデルから出力される結果のこと
モデルに予測させたいデータのこと
教師あり学習とは?
教師あり学習とは
- 入力データ
- 出力データ
のセットを与えて学習させる方式。
例えば、よくあるのでいうとアイスクリーム屋の売上を
気温から予測するモデルを作りたい場合は
データとして
- 気温(入力データ)
- 売上(出力データ)
を与えて学習させる。
そうすると気温を与えれば売上を予測してくれる
モデルが完成する。
単回帰分析とは?
1種類の説明変数に対して、目的変数を予測する分析のこと。
上のアイスクリーム屋の例でいうと説明変数は「気温」、
目的変数は「売上になる」
機械学習モデルの単回帰分析ついて簡単な数式で 表してみる。
数式
数式にすると下記のようになる。
y = Ax + B
yが売上でxが気温になるイメージ
用語と照らし合わせていくと
機械学習モデル(機械学習アルゴリズム)
モデルとアルゴリズムはほぼセットなので
y = Ax + Bこの数式自体がモデル。 選択した機械学習アルゴリズムによって数式が変わる。
目的変数
数式でいうと目的変数は「y」になる。
y = Ax + Bモデルである数式を計算した結果が目的変数となる
説明変数
数式でいうと説明変数は「x」になる。
y = Ax + B
モデルである数式に渡す値が説明変数となる
パラメータ
数式でいうとパラメータは「A」、「B」になる
y = Ax + B
傾きと切片がパラメータとなる。 このパラメータを学習することで確定させる
モデルに学習させるとは?
つまり教師あり学習でモデルに学習させるというはx(説明変数)とy(目的変数)の組み合わせのデータを
与えてAとB(パラメータ)を求める作業になる。
AとBの値が学習によって定まれば、新しいx(説明変数)を入力すればy(目的変数)
を計算によって算出できようになる。
この計算可能になった状態のモデルを学習済みモデルという。
Pythonで機械学習をする準備
実際にPythonを使って線形単回帰分析を実装してみる。
開発はDockerで作ったPython環境でVScodeを
使って行う
Pythonの開発環境を作る
まずはPythonの開発環境を作る
作り方は下記の記事でまとめています
※DockerとVScodeで環境構築しています
公式のpython.orgから作る場合
Anacondaから作る場合
データサイエンスや機械学習に関連する多数のパッケージが同梱されている
※Anacondaは商用利用する場合は有償になるので注意!!
今回は「公式のpython.orgから作る」でやっていく!
ライブラリのインストールをする
機械学習で単回帰分析をするために必要なライブラリをインストールする
下記はとりあえず入れておいてもいいと思う
numpy
数値計算を効率的に行うためのライブラリ
pandas
大量データをまとめて操作し、整理するためのライブラリ
matplotlib
データの可視化に使うグラフなどを描写するためのライブラリ
numpyやpandasで操作したデータを可視化したりできる
seaborn
seabornもPythonでグラフを作るためのライブラリ
scikit-learn
Python用の機械学習ライブラリ
このライブラリで機械学習モデルを作り
学習させる
pip install numpy pandas matplotlib seaborn scikit-learn
Pythonで機械学習(単回帰分析)を実装する
Pythonで機械学習(単回帰分析)をする環境が整ったので
実際に実装していく
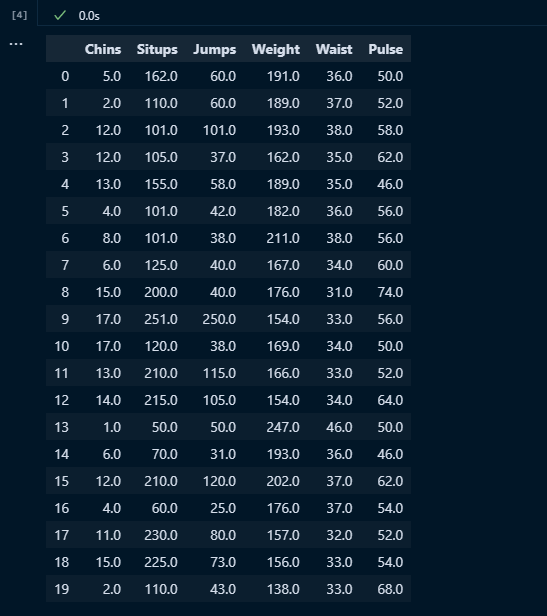
使用データ(生理学的データと運動能力の関係のデータセット)
scikit-learnのサンプルデータの
- 生理学的データと運動能力の関係のデータセット
を使う。
x(説明変数)データ
- Chins : 懸垂の回数
- Situps : 腹筋の回数
- Jumps : 跳躍の回数
Chins Situps Jumps0 5.0 162.0 60.01 2.0 110.0 60.02 12.0 101.0 101.03 12.0 105.0 37.04 13.0 155.0 58.05 4.0 101.0 42.06 8.0 101.0 38.07 6.0 125.0 40.08 15.0 200.0 40.09 17.0 251.0 250.010 17.0 120.0 38.011 13.0 210.0 115.012 14.0 215.0 105.013 1.0 50.0 50.014 6.0 70.0 31.015 12.0 210.0 120.016 4.0 60.0 25.017 11.0 230.0 80.018 15.0 225.0 73.019 2.0 110.0 43.0
y(目的変数)データ
- Weight : 体重
- Waist : ウエスト
- Pulse : 脈拍
Weight Waist Pulse0 191.0 36.0 50.01 189.0 37.0 52.02 193.0 38.0 58.03 162.0 35.0 62.04 189.0 35.0 46.05 182.0 36.0 56.06 211.0 38.0 56.07 167.0 34.0 60.08 176.0 31.0 74.09 154.0 33.0 56.010 169.0 34.0 50.011 166.0 33.0 52.012 154.0 34.0 64.013 247.0 46.0 50.014 193.0 36.0 46.015 202.0 37.0 62.016 176.0 37.0 54.017 157.0 32.0 52.018 156.0 33.0 54.019 138.0 33.0 68.0
ただ今回は単回帰分析をするため上記の
xとyのデータから1列ずつにする
x(説明変数)データ~件数の回数のみ~
Chins0 5.01 2.02 12.03 12.04 13.05 4.06 8.07 6.08 15.09 17.010 17.011 13.012 14.013 1.014 6.015 12.016 4.017 11.018 15.019 2.0
y(目的変数)データ~体重のみ~
- Weight : 体重
Weight0 191.01 189.02 193.03 162.04 189.05 182.06 211.07 167.08 176.09 154.010 169.011 166.012 154.013 247.014 193.015 202.016 176.017 157.018 156.019 138.0
1列ずつにしたデータセットを使って
懸垂の回数から体重を予測できる機械学習モデルを作る!
数式にすると
体重 = 懸垂の回数 x A + B
のような感じ。
データを使ってモデルに
パラメータであるAとBの値を学習させれば
懸垂の回数がわかれば、体重の予測ができるようにする
完成ソースコード
最初に完成したソースコードを載せる
# 必要なライブラリ等にimportfrom sklearn.datasets import load_linnerud #testdatafrom sklearn.model_selection import train_test_split # 分割メソッドfrom sklearn.linear_model import LinearRegression # モデルimport seaborn as snsimport matplotlib.pyplot as plt# データ取得# Dataframe型で取得df = load_linnerud(as_frame=True).frame# 必要な列を抽出(件数の回数と体重)df_edit = df[['Chins','Weight']]# 説明変数をセット(ndarray)に変換# x = filterddf['Chins'].values.reshape(-1, 1)x = df_edit[['Chins']].values# 目的変数をセット(ndarray)に変換# y = filterddf['Weight'].values.reshape(-1, 1)y = df_edit[['Weight']].values# データセットの分割# 学習用データセットを作成# 学習データ7割、テストデータ3割x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.4,random_state=0)# モデルの定義# どの機械学習アルゴリズムを使うかmodel = LinearRegression()# モデルに学習させるmodel.fit(x_train,y_train)# パラメータの確認(定まっているか)model.coef_# 切片の確認model.intercept_# モデルの検証# テストデータを使う# 決定係数(最大値が1※1に近いほど茣蓙が少ない)print(f'train_score:{model.score(x_train,y_train)}')print(f'test_score:{model.score(x_test,y_test)}')# モデルに予測させるy = model.predict(x_test)# 予測値と実績値の比較print(f'予測値:{y[0]} 入力値:{x_test[0]}')print(f'実測値:{y_test[0]} 入力値:{x_test[0]}')# グラフの描画# 散布図sns.scatterplot(data=df,x='Chins',y='Weight')# 回帰線付き散布図sns.lmplot(data=df_edit,x='Chins',y='Weight')
細かいところは後述で解説していく
データを読み込む
機械学習モデルに学習させるためのデータを読み込む
# 必要なライブラリ等にimportfrom sklearn.datasets import load_linnerud #testdatafrom sklearn.model_selection import train_test_split # 分割メソッドfrom sklearn.linear_model import LinearRegression # モデルimport seaborn as snsimport matplotlib.pyplot as plt# データ取得# Dataframe型で取得df = load_linnerud(as_frame=True).frame
説明変数である
- Chins
- Situps
- Jumps
と目的変数である
- Weight
- Waist
- Pulse
が一つの表(テーブル)になっている
データの編集
モデルに学習させるために上記のデータを
xとyに分ける
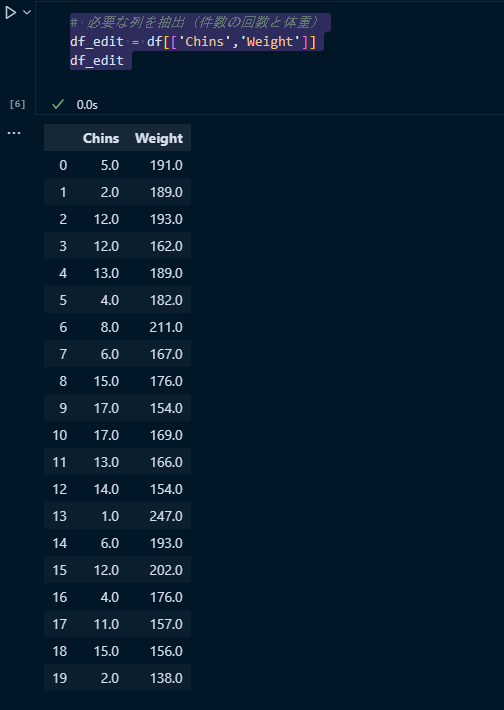
データの抽出
まずは対象となるデータを抽出する
# 必要な列を抽出(件数の回数と体重)df_edit = df[['Chins','Weight']]
説明変数を設定
懸垂の回数を説明変数に設定する
# 説明変数をセット(ndarray)に変換x = df_edit[['Chins']].values# array([[ 5.],# [ 2.],# [12.],# [12.],# [13.],# [ 4.],# [ 8.],# [ 6.],# [15.],# [17.],# [17.],# [13.],# [14.],# [ 1.],# [ 6.],# [12.],# [ 4.],# [11.],# [15.],# [ 2.]])
xに説明変数として懸垂の回数を設定する
注意点としては上記のように2次元の配列になっている必要がある
なぜかといういうと、例えば
x = df_edit['Chins'].values# array([ 5., 2., 12., 12., 13., 4., 8., 6., 15., 17., 17., 13., 14.,# 1., 6., 12., 4., 11., 15., 2.])
のように1次元の配列にしていた場合
モデルに入れる時に
「ValueError: Expected 2D array, got 1D array instead:」
のエラーがでて怒られるため。
目的変数を設定
体重を目的変数に設定する
# 目的変数をセット(ndarray)に変換y = df_edit[['Weight']].values# array([[191.],# [189.],# [193.],# [162.],# [189.],# [182.],# [211.],# [167.],# [176.],# [154.],# [169.],# [166.],# [154.],# [247.],# [193.],# [202.],# [176.],# [157.],# [156.],# [138.]])
こちらも同様に2次元の配列になっている必要がある
データセットの分割
モデルに学習させるためにデータセットを分割する
要は今作ったx,yのデータを7割をトレーニング用データとして
モデルを学習させるために使い、
残りの3割を学習済みモデルのテストに使うといった感じ
# データセットの分割# 学習用データセットを作成# 学習データ7割、テストデータ3割x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.3,random_state=0)
sklearn.model_selectionの「train_test_split」というメソッドを
使うとできる
- x_train(xの学習データ)
- x_test(xのテストデータ)
- y_train(xの学習データ)
- y_test(yのテストデータ)
random_state=0はそれを設定しておく
※0以外を設定するパターンを知らない。。。。
モデルの定義
使う機械学習モデルを定義する
今回は単回帰分析なのでsklearn.linear_modelの
- LinearRegression
を使う
# モデルの定義# どの機械学習アルゴリズムを使うかmodel = LinearRegression()
モデルの選択はデータを見て人間が行う必要がる
モデル学習
データの準備と使うモデルが決まったので
モデルに学習させて学習済みモデルにする
# モデルに学習させるmodel.fit(x_train,y_train)
モデルに学習させるにはfitメソッドを使う
引数としては分割したうちの学習用データを与える。
実行すれば学習が完了する
※何か意外と学習ってずぐできるのね。。
学習済みモデルの確認
学習済みモデルになったので
数式
y = Ax + B
のAとBのパラメータが定まっているので確認する
傾き(A)を確認する
# パラメータの確認(定まっているか)model.coef_# array([[-1.40909091]])
パラメータはcoef_で確認できる
切片(B)を確認する
# 切片の確認model.intercept_
切片はintercept_で確認できる
これでどうやら数式は完成したようだが
この数式が正しいか、というかちゃんとした予測ができるか
わからないので学習済みモデルの評価をする必要がある
モデルの検証
データを学習した学習済みモデルが精度の高い予測ができるか
どうか検証する
検証には分割したデータのテストデータの方を使う
# モデルの検証# 決定係数(最大値が1※1に近いほど茣蓙が少ない)# テストデータprint(f'test_score:{model.score(x_test,y_test)}')# 学習データprint(f'train_score:{model.score(x_train,y_train)}')# 決定係数# test_score:0.13764136222823264# train_score:0.1477906158845732
scoreメソッドで決定係数を求めることができる
決定係数は1に近い程良い。
この結果を見ると精度は全然のようだ。 ※データの列削っているし、データ数も少ないので。。
モデルで予測
精度は全然ダメみたいだが、一応、このモデルを使って
予測をしてみる
予測をせさるにはpredictメソッドを使う
# モデルに予測させるmodel.predict(x_test)
データはテストデータを使う
結果をみてみる
# 予測値と実績値の比較print(f'予測値:{y[0]} 入力値:{x_test[0]}')print(f'実測値:{y_test[0]} 入力値:{x_test[0]}')# 予測値:[170.13636364] 入力値:[15.]# 実測値:[156.] 入力値:[15.]
入力値:[15.]に対して、モデルが予測したのは
「170.13636364」
対して実際の値は
「156.」
なので、決定係数通り、全然当たってない。
とまぁ、実際に作ったモデルは全然ダメだったわけだが
機械学習の教師あり学習の流れはこんな感じになる
グラフの描画
コードだけだとわかりづらいし、グラフでも描画してみる
散布図
データの散布図を描画してみる
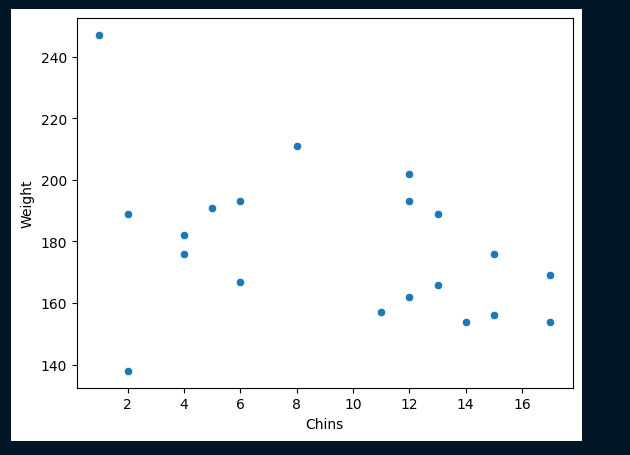
# グラフの描画# 散布図sns.scatterplot(data=df,x='Chins',y='Weight')
x軸に懸垂の回数 y軸に体重とする
なんとなく懸垂の回数が多くなる程、体重が
軽くなっているように見える
回帰線付き散布図
回帰線付きの散布図を書いてみる
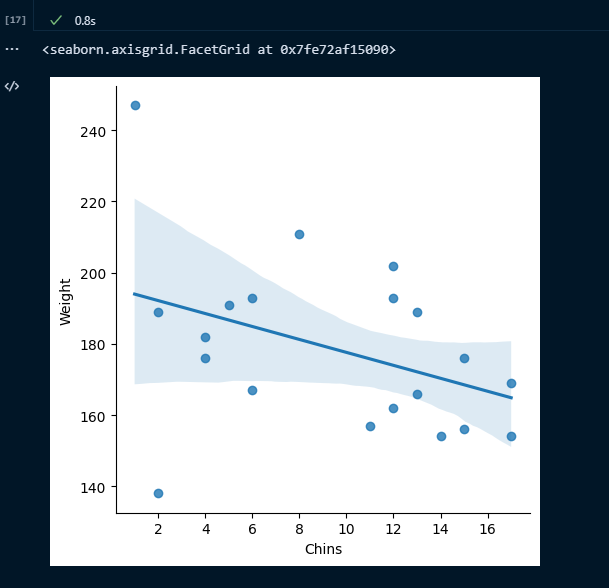
# 回帰線付き散布図sns.lmplot(data=df_edit,x='Chins',y='Weight')
ただやはり圧倒的にデータが少ない。。。
まとめ
Pythonを使って機械学習の教師あり学習(単回帰分析)を
実装してみた。
無理やり単回帰にしたためか、データが少なかったのかわからないが
モデルとしてはよくないものになっていしまった。
ただ、機械学習をさせるための基本的なデータの準備からモデルで予測させる
ためのフローは理解することができたと思う
今後も知識が増えたらまた色々、記事にまとめていきたい。